A first example – Encryption and Decryption
4.3.1 A first example
Let’s construct an example of a perfectly secret encryption scheme based on these requirements. It will also help you get a grip on the ingredients of a symmetric cryptosystem given in the previous section.
We want to encrypt the roman letters a,b,g by mapping them onto their counterparts in the greek alphabet α,β,γ. Formally, this means that ℳ = {a,b,g} and 𝒞 = {α,β,γ}. Because of requirement 1, we will also need three keys, so let’s say 𝒦 = {1,2,3}. Now we need three encryption functions e1,e2,e3, all having ℳ = {a,b,g} as domain and 𝒞 = {α,β,γ} as co-domain. We can find them by observing requirement 2.
We start by defining e1 by its action on the elements of ℳ: e1(a) = α,e1(b) = β,e1(g) = γ. Note that each element of 𝒞 appears on the right-hand side of exactly one equation. Had we defined e1(b) to be α instead, the resulting function would not have been bijective.
For e2, we need to change something. We cannot simply repeat the definition for e1, because in this case, we would not be able to satisfy requirement 2 (remember there are only three encryption functions overall). So let’s switch to new plaintext-ciphertext pairs, by saying e2(a) = β,e2(b) = γ,e2(g) = α. Note again that e2 is bijective.
Looking at the pairs we have defined so far, we see there are only three plaintext-ciphertext pairs left. They define the third encryption function: e3(a) = γ,e3(b) = α,e3(g) = β.
And we are done! The action of the decryption functions d1,d2,d3 can be deduced by following the arrows in Figure 4.7 from right to left. For a truly perfectly secret cryptosystem, we only need to take care that all three keys are chosen with equal probability, that is 1∕3 in this case.
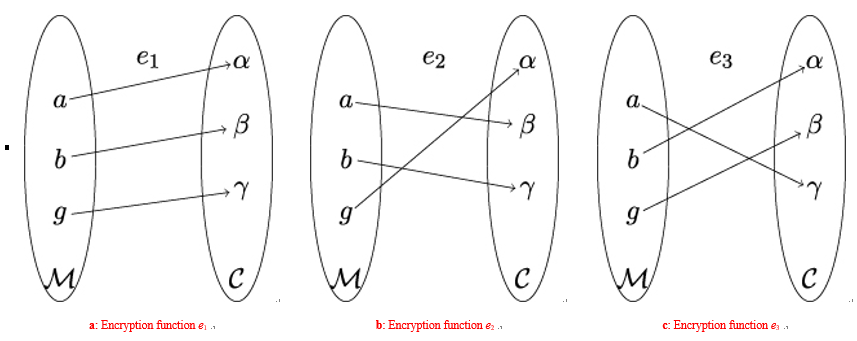
Figure 4.7: The three encryption functions constructed in our example
We can even check for ourselves that this cryptosystem is perfect. Let’s assume that Eve observes the cipher c = γ on the channel. From her knowledge of the plaintext space ℳ alone, she has a probability of 1∕3 of guessing the correct plaintext.
Because of Kerckhoff’s principle, however, we must also assume that Eve knows exactly how the encryption functions e1,e2, and e3 work. By analyzing them, Eve can, for example, deduce that the following relation holds:
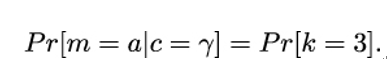
This is because only e3 maps a onto γ. But all keys occur with equal probability, so the probability that a is the plaintext after Eve has observed the ciphertext γ is 1∕3, the same as her guessing probability.

