Asymptotic approach and efficient computation – Encryption and Decryption
4.4.1 Asymptotic approach and efficient computation
To account for future advances in computing technology, software or hardware optimized for a specific type of attack, and potential differences in the desired security level (e.g., average internet user versus government agency), modern cryptography uses a so-called asymptotic approach rooted in complexity theory [97].
The asymptotic approach treats the execution time of an attack as well as Eve’s probability to succeed with that attack as functions of the so-called security parameter n, which is simply the key length in many cases. When Alice and Bob initialize the encryption scheme – for instance, when they exchange the secret key k – they choose a specific value for n (in practice, they choose a particular standardized variant of that encryption scheme with n having a pre-defined length, e.g., 128, 256, or 512 bits).
A polynomial p is a special kind of function that can be written in the form
for some numbers ai and input n.
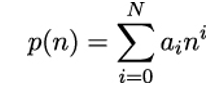
An algorithm A is said to run in polynomial time if we can find a polynomial p, so that for any input x to A of length n, the computation of A terminates after at most p(n) steps, which means we are always looking at bounds for the worst case.
Polynomials are used to classify the running time of an algorithm, because they grow with their input in a controllable way. In most cases (as in this section), we are only interested in the asymptotic behavior of the polynomial (that is, the growth for very large n. This behavior is governed by the largest power of n appearing in the polynomial (its degree N). If, for example, the running time of an algorithm can be described by a polynomial of degree 3, we say the algorithm is in 𝒪(n3).
In complexity theory, the terms efficient and polynomial running time are often used synonymously for algorithms. Thus, in the context of computational security, efficient (attack) algorithms that Eve can execute in a practically feasible amount of time are probabilistic algorithms having a runtime that is polynomial in n [97].
In other words, for an efficient algorithm, there must be some constants a,c, so that the running time T increases like a ⋅ nc with the security parameter n. Any attack algorithms that require a super-polynomial amount of time are ignored because they are not considered to be realistic threats.
A probabilistic or randomized algorithm is one that employs a degree of randomness as part of its logic or procedure [195]. Such algorithms effectively have the capability of making random decisions, which makes them non-deterministic.
The reason probabilistic algorithms are used in the context of computational security is that they can be faster than their deterministic counterparts. Even if this is not guaranteed, we can ignore them in our assessment of the security of an encryption scheme. Quicksort, a well-known algorithm for in-place sorting, is a good example of this phenomenon (which is not limited to cryptanalysis).
Quicksort is a divide-and-conquer algorithm that sorts an array by selecting a so-called pivot element from that array and partitioning the other elements into two sub-arrays depending on whether they are less than or greater than the pivot [194]. It can be mathematically shown that Quicksort is more likely to finish faster if it selects the pivot elements uniformly at random.
The fact that probabilistic algorithms could finish in fewer steps makes them more suitable for modeling the capabilities of an attacker as they allow to make a more conservative assumption from the defender’s point of view. To be sure, any encryption scheme that is secure against a probabilistic polynomial time attack is also secure against its deterministic version [97].

