Stream ciphers – Encryption and Decryption
4.5.1 Stream ciphers
Using a pseudorandom generator, we can construct a symmetric cryptosystem, shown in Figure 4.9. By looking closely at the lower part of the figure, you’ll recognize that this cryptosystem emulates the one-time pad encryption discussed earlier in this chapter. However, unlike the original one-time pad, this encryption scheme uses a short truly random string K (the key) instead of the much longer pad, which needs to have the same length as the message to be encrypted. This kind of cryptosystem is called a stream cipher. Here, the pseudorandom generator G is used to produce a random-looking stream of key bits, which is in turn used to encrypt plaintext m by XORing it with the pseudorandom pad k, just like in the one-time pad.
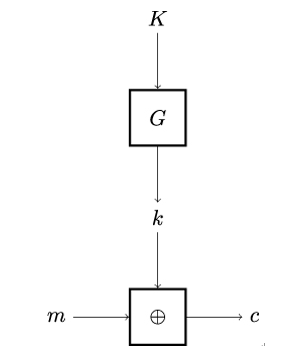
Figure 4.9: Computationally secure encryption scheme based on a pseudorandom generator
The XOR operation ⊕ in Figure 4.9 – that is, the encryption operation itself – uses the pseudorandom string k obtained from the pseudorandom generator G. Because no polynomial-time algorithm can distinguish between a pseudorandom and a truly random string, this encryption scheme is computationally secure against eavesdropping attackers (so-called ciphertext-only attacks) [97]. Of course, for stream ciphers the same limitation applies as for the one-time pad: the key stream k must not repeat or be reused, otherwise, we run into the problems shown in Equation 4.3.2.
4.5.2 RC4
RC4 is a stream cipher that was very popular in the past because of its simplicity, speed, and apparent security. It also found heavy use within TLS until around 2013, when practical attacks on it were published [3]. As a consequence, use of RC4 within TLS was prohibited in 2015. The reason for discussing it here is to provide a relatively simple example of the inner working of a stream cipher. Later in this book, when discussing the modes of operation of block ciphers in Chapter 14, Block Ciphers and Their Modes of Operation, we will get to know more secure ways to construct stream ciphers.
The following description of RC4 is based on the account in [158]. RC4 consists of a state array S holding 256 bytes Si, which are filled linearly at the beginning: Si = i,0 ≤ i ≤ 255. The initial seed, or key K consists of ℓ bytes Kj, where each key byte is written as a number between 0 and 255 and is used to address the entries of the state array. With the help of K, the state array is shuffled by selecting certain entries and swapping them:
for 0 ≤ i ≤ 255 do
Si ← i
end for
j ← 0
for 0 ≤ i ≤ 255 do
x ← i (mod ℓ)
j ← (j + Si + Kx) (mod 256)
swap Si and Sj
end for
After the initial shuffling phase, S is further shuffled and one byte St is selected to encrypt the first plaintext byte via bitwise XOR. After that, the shuffling and byte selecting go on until all N plaintext bytes Pn have been encrypted to cipher bytes Cn:
i ← 0
j ← 0
for 1 ≤ n ≤ N do
i ← (i + 1) (mod 256)
j ← (j + Si) (mod 256)
swap Si and Sj
t ← (Si + Sj) (mod 256)
Cn ← Pn ⊕ St
end for
The effect of encrypting a file by RC4 can be nicely visualized by applying it on a grayscale image (see Figure 4.10). In a grayscale image, each pixel has a luminance value between 0 and 255 (i.e., it is a byte), therefore we can simply encrypt the luminance values pixelwise using the RC4 output.
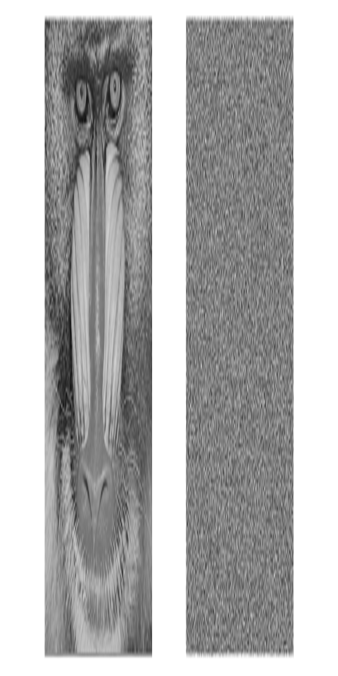
Figure 4.10: Encrypting a grayscale image with RC4
Obviously, all visual structure has disappeared from the cipher image. But the cipher image also looks random at a statistical level (see Figure 4.11 and Figure 4.12):
- While the distribution of luminance values in the plaintext image has a distinct shape, in the cipher image basically all luminance values occur with the same frequency, as they should in a random image. This results in the flat histogram on the right of Figure 4.11.
- In natural images, the luminance values of neighboring pixels are strongly correlated. The encryption process destroys this correlation, as Figure 4.12 shows for the case of horizontally neighboring pixels. Similar figures could be produced for vertically or diagonally neighboring pixels.
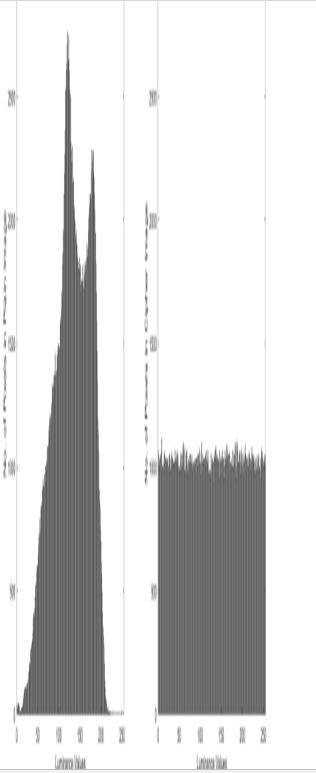
Figure 4.11: Frequency distribution of luminance values. Left: plaintext image; Right: cipher image

Figure 4.12: Correlation of 3,000 randomly selected, horizontally neighboring pixels. Left: plaintext image; Right: cipher image
For Figure 4.12, the luminance values of 3,000 randomly selected pixels were compared to their horizontal neighbors. In a natural image, the luminance changes slowly and therefore the luminance values of neighboring pixels tend to be largely the same. In a cipher image, on the other hand, there should be no correlation left, and this is clearly shown on the right-hand side of the figure.
We’ll now discuss a new kind of attack, where Eve can feed plaintexts of her choice to an encryption server.

