The one-time pad – Encryption and Decryption
4.3.2 The one-time pad
The prime example of a perfectly secret encryption scheme is the so-called one-time pad, also known as the Vernam cipher.
It was first described by Frank Miller in 1882 and re-invented by Gilbert Vernam in 1917, who also patented the cipher in 1919. The original version of the Vernam cipher had a cryptographical weakness because the bits on the key tape were reused after having been used once. The one-time use of the key tape was introduced later by Joseph Mauborgne who conjectured that cryptanalysis would be impossible if the key bits were completely random and never reused [192]. About 25 years later, Claude Shannon, was able to show mathematically that the one-time pad is indeed perfectly secret.
The one-time pad can be easily described in terms of the previous example. Here, ℳ = 𝒞 = 𝒦 = {0,1}. The encryption functions are e0 and e1, where e0(0) = 0,e0(1) = 1 and e1(0) = 1,e1(1) = 0. In this case, there is, however, a more compact way to describe the encryption process: We can write it as
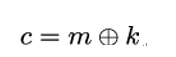
where ⊕ denotes a bit-wise exclusive OR (XOR) operation. If you take two bits b0,b1 and apply the XOR operation onto them, b0 ⊕ b1 will yield zero whenever both bits have the same value (that is, both are zero or both are one) and one whenever the bits have a different value.
So far, we have only considered encrypting single bits. If the plaintext m consists of l bits, we simply repeat the encryption process l times, where each time the key bit k is chosen randomly. If we slightly extend our notation for the key k to mean a random bitstring of length l, we may write again
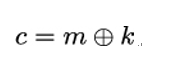
where m, c, and k are all bitstrings of length l.
Likewise, the decryption operation in the one-time pad scheme is performed by computing
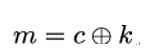
To re-iterate, the one-time pad is perfectly secret because, if Eve observes a ciphertext c, she is unable to get additional information about the corresponding plaintext m from c. This is because for every possible m we can find a corresponding key k such that c = m ⊕ k.
In addition, every key occurs with the same probability, so no key has a higher probability than the others. As a result, every possible m is equally likely to have been encrypted and the ciphertext c reveals nothing about the plaintext.
As you might have guessed though, perfect secrecy – like most things in cryptography – is a trade-off. There is no free lunch, and a number of very inconvenient requirements for all practical purposes must be fulfilled for perfect secrecy to work.
First, the secret key must be as long as the message to be encrypted. This not only makes it more difficult to securely store the key, but also means that Alice and Bob must securely exchange the same amount of information that they are going to encrypt beforehand. But then – since they must exchange a secret key that is as long as the message – they can also exchange the message itself.
In other words, a perfectly secure scheme like the one-time pad effectively only allows encryption in the ”time domain”: if Bob manages to securely get an l-bit secret key to Alice today, she can use that key tomorrow to encrypt an l-bit message for Bob.
Second, to remain secure, every key can be used only once – that’s why it is called the one-time pad. Using the same key k twice immediately leaks information because:
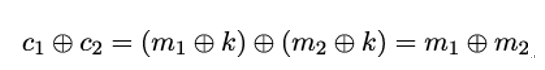
This is a problem if certain parts or statistics about m1 or m2 are known. This knowledge can then immediately be transferred to the other message.
For these reasons, the one-time pad is very rarely used in practice. It remains important, however, to know that such a thing as a perfectly secure cipher actually exists. For other, not perfectly secure encryption schemes, it provides a benchmark to strive for.

